Energy Storage Systems

Zezhang Yang
SUNY-Binghamton University
Binghamton, NY, USA
zyang80@binghamton.edu

SaLisa Berrien
COI Energy
New York City, NY, USA
salisa@coienergy.com

Jian Li
SUNY-Binghamton University
Binghamton, NY, USA
lij@binghamton.edu

Abstract—Large and stochastic peak energy demands of buildings contribute to grid inefficiency. Here, we present an optimization algorithm for behind-the-meter peak shaving with energy storage systems. We employ a Markov decision process to execute charging and discharging decisions on sub-hourly time scales according to the on-site energy profile and the size of the energy storage system. The algorithm minimizes the peak load drawn from the grid to maximize savings for the asset owner and efficiency gains for the grid network. Our technology-agnostic solution can serve battery energy storage systems and lesser-studied use cases including pumped hydro storage and municipal water systems. We demonstrate how the algorithm can inform on sizing energy storage systems to best serve a given building. With these contributions, we provide an AI platform to optimize energy storage assets and smart grid systems.
Index Terms—artificial intelligence, demand-side management, energy storage, optimization, smart grid

I. INTRODUCTION

Rapid population growth and technological progress has greatly increased the demand for energy [1] [2]. The unsustainable nature of fossil fuels has driven the energy market to cleaner sources. Locally distributed renewable energy generation offers eco-friendly power with the primary drawback of intermittent output [3] [4]. Likewise, many countries have focused on improved efficiency due to recognizing that renewable energy sources are less capable to support the prevalent energy waste that exists today [5].
The transition to renewable energy requires integrated energy storage to serve continuous loads and high peak demands [6] [7]. A diverse and optimally-managed portfolio of energy storage systems will greatly increase the reliability and cost- effectiveness of a net zero energy network [8]. Such storage devices ideally charge with excess renewable energy, discharge when systemic demand is highest or intermittent output is lowest, and incur minimal losses during energy storage and dispatch.
Currently available energy storage technologies include batteries, pumped hydro, compressed air, flywheels, and thermal energy storage. While batteries receive the most attention, pumped hydropower storage (PHS) remains the most mature and widely-applied method for large electricity storage, with global PHS capacity of 165 GW, including 25 GW of hybrid power plants [8] [9] [10]. PHS benefits from high round-trip efficiency, long-duration (seasonal) energy storage, and

fast ramping of power input/output [11]. These favorable characteristics have inspired much research around PHS. For instance, Bin Lu et al. [12] [13] found enormous global potential for PHS, yet did not provide a detailed analysis of costs or water availability. At smaller scales, Rogeau et al. [14] quantified the potential for PHS systems in Europe and Ghorbani et al. [15] investigated the potential for PHS systems in Iran.
Crucially, these prior efforts overlooked the potential for leveraging PHS within municipal infrastructure. For example, the US consumes 260 billion kilowatthours (kWh) annually to power municipal water systems [16]. Even in the absence of direct energy generation, water-based infrastructure can leverage existing tanks to elevate water in off-peak hours and allow systems to run off gravity during on-peak hours. Such peak shaving is an important technique to improve systemwide energy efficiency [17].
Here, we present a simple and universal algorithm for managing behind-the-meter (BTM) energy storage and pumped hydro systems. We use a Markov Decision Process to store power (fill tanks) during low-demand hours and discharge power (empty tanks) during high-demand hours. We dynamically control the charge and discharge rates with 15-minute granularity to manage assets in conjunction with standard demand billing practices. As such, we maximize BTM peak shaving to reduce customer costs and grid capacity requirements. We present simple inputs which are easily defined for real-life battery, PHS, or other energy storage systems. We validate the peak shaving optimization algorithm using data from a commercial building.

II. ENERGY STORAGE MODEL

In this section, we describe our optimization approach for BTM peak shaving. Because of its ability to align with electricity billing practices, we employ the discrete-time Markov Decision Process (MDP) [18]. MDP provides a mathematical framework to execute a decision-making strategy which discretely controls predictable and partly random outcomes. Past works demonstrated the effectiveness of MDP in diverse applications including utility resource management, third-party supply chains, and customer service [19]. In testing our algorithm, we derive increments of energy demand from

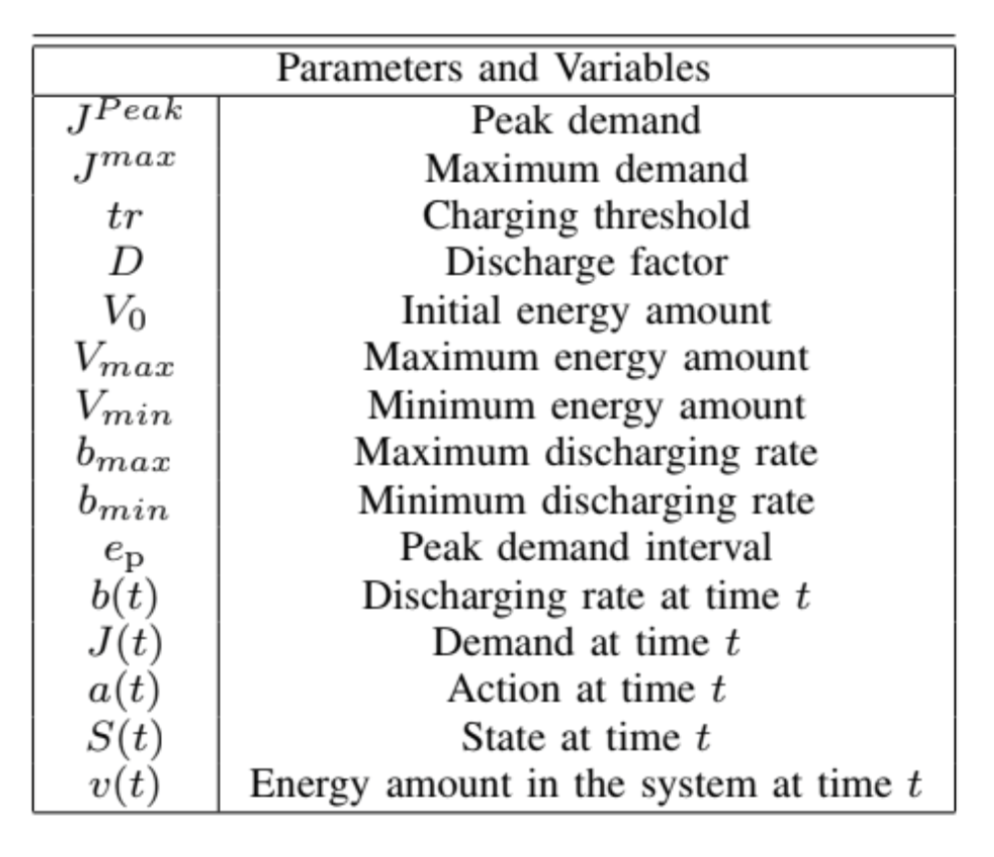
TABLE I
THE LIST OF PARAMETERS AND VARIABLES

continuous energy usage data to yield a series of discrete time states that is well-suited for MDP-based controls.

A. Overview of the Energy Storage Model
The MDP optimization provides a signal to control the state of the storage system with the objective to shave the peak load of the BTM energy account. The technology-agnostic algorithm can serve batteries, PHS facilities, municipal water networks, and more. The MDP considers a single-day scale, assuming that energy will always be abundant/cheap in off- peak hours and scare/expensive in on-peak hours. Before each day, the BTM demand is forecasted to provide a signal for MDP optimization. The optimization depends on the so-called charging threshold, an activation parameter which classifies a given time unit as on- or off-peak. The energy storage system will charge or discharge based on how the BTM load compares to the threshold value. This model can manage energy storage with fast response times and limited energy capacities. It is easily tuned to consider a specific system without compromising the accuracy of the optimization procedure.

B. Static Parameters
Pursuant to managing the energy storage every day, we assume that an off-peak demand period (e.g. overnight) always follows a peak demand period (e.g. afternoon). Additional constraints can allow for multi-day discharge if excess energy is unavailable. We dynamically tune our energy storage control throughout the working time to best satisfy the objective of reducing peak demand. This simplifies against prior approaches that account for dynamic energy price fluctuations, since end-use consumers are not necessarily exposed to market prices and realize significant cost savings by shaving peak consumption. It also ensures demand management that is universally online, since monthly billing cycles mean that a single failure can obviate a prior month of savings.
The list of parameters used to characterize the model is summarized in Table I. These parameters are deliberately technology-agnostic. Energy may refer to the charge state of an electric battery, the fill level of a water tank, or the temperature of a thermal battery; charge rates may be determined by

inverter systems, water tank heights, or heat transfer elements. Even in the absence of a hydroelectric generator, municipal and industrial water systems are within the scope of this energy optimization due to the ability to shift load by pre-pumping water into elevated tanks and reducing subsequent energy inputs.

C. State Variables
Let T = t₀, t₁, …, t_t be the time set within a day and let ∆t denote the increment between t_t and t_t−1. We define S_t = (f^peak, J(t), v(t), b(t)) as a vector of time t decision variables. f^peak is the peak demand identifier, a binary factor set to f^peak = 1 when J(t) ∈ J^Peak. At all other times, f^peak = 0. We define J^Peak = {J(t)J(t) < J^max × tr}, where J(t) is the current demand at time t, v(t) is the current energy amount at time t, and b(t) is the power injected by the storage system at time t.
At every time, the storage system will charge, discharge, or do neither as per best satisfying the peak-shaving objective. The system will ingest energy when S(t) satisfies the conditions f^peak = 0, J(t) ≠ J^Peak, v(t) < V_max, b(t) < 0. The system will discharge energy when S(t) satisfies the conditions f^peak = 1, J(t) = J^Peak, V_min < v(t), b(t) > 0. Finally, the system will hold its current energy level when S(t) satisfies the conditions f^peak = 1, J(t) = J^Peak, V_min =v(t), b(t) = 0. This holding condition means that the storage system is fully energized or de-energized and awaiting a more optimal time to switch states.

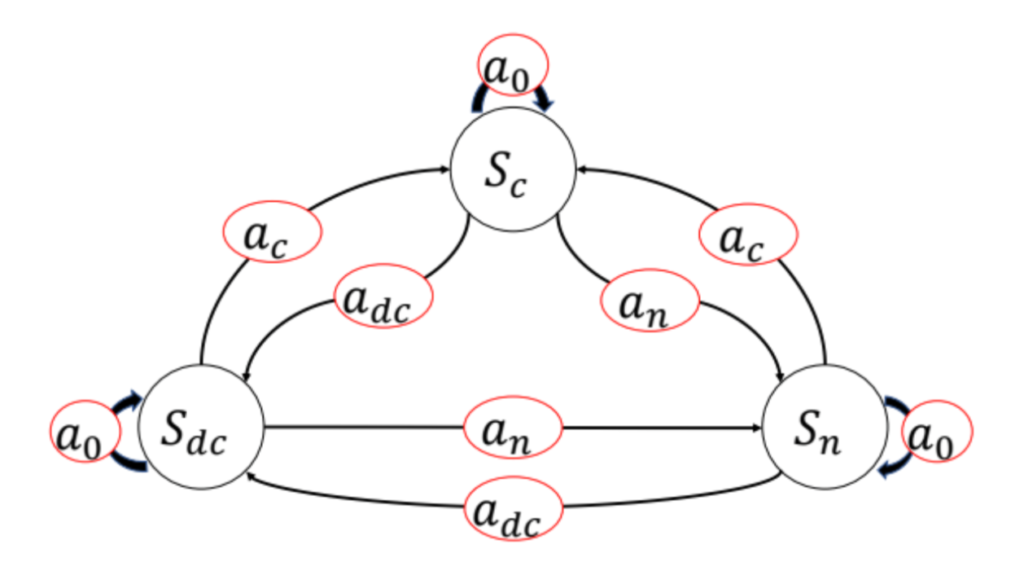
D. Actions
At every time step t, the storage management decision is given by the vector a(t) = (e_t^dc, e_t^c), where e_t^dc represents energy discharge and e_t^c represents energy charge at time t. The mutually exclusive actions capture the charge and discharge rate of the storage system. A positive value of a_t means the storage system injects energy into the BTM load, relieving strain on the grid. A negative value of a_t means the storage system ingests energy for future injection. The algorithm executes one of four actions: begin charging a_c , where a(t) = (e_t^dc = 0, e_t^c); begin discharging a_dc , where a(t) = (e_t^dc, e_t^c = 0); halt charging or discharging a_dc , where a(t) = (e_t^dc = 0, e_t^c = 0); and maintain previous state a0,

where a(t) = a_t−1. The decision states are constrained by requiring that the total amount of energy stored in the device does not exceed its energy capacity: V_min < v(t) < V_max. The relationships between states and actions are illustrated in
Figure 1.

E. State Transition Function
The energy in the storage system v(t) evolves according to the following transition equations v(t + 1) = v(t) + b(t). The energy amount at time t+1 is decided by the energy amount at time t and the charging or discharging amount during time t. For simplicity, energy transduction is considered lossless and the storage mechanism is unconstrained by cycling frequency. These assumptions are more valid for PHS than for battery systems and can be modified as needed.

F. Constraints
The on-peak demand interval is defined as the time period where the BTM load exceeds the value of the charging threshold multiplied by the maximum demand: tr × J_max:

The current power remaining in the storage system is determined by initial energy in the storage system and the power ingested/injected by the storage system:

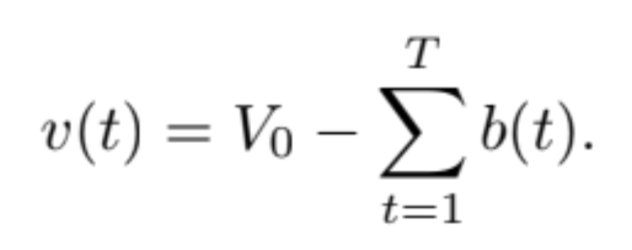
(2)

The current power remaining in the storage system is constrained by the system’s capacity limits:

G. Objective Function
The objective function’s goal is to shave the maximum BTM demand by discharging energy during the on-peak period and recharging energy during the off-peak period. The peak shaving achieved in time t is given by:

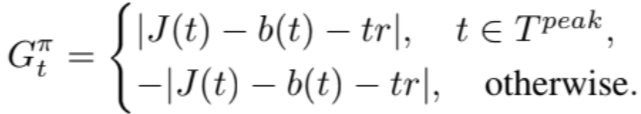
(4)

Because the storage system profit is directly related to the maximum BTM load, the optimized system profit will be:

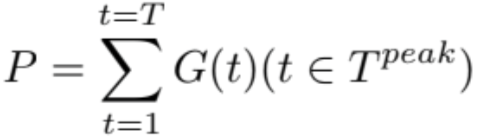
(5)

In the profit formulation, we neglect time-sensitive energy rates because these differences are often small when compared to peak demand costs. Since energy is cheaper in off-peak periods, the profit estimations undersell the complete financial incentive for optimized energy storage. The objective for each time t is to determine an optimal policy π^∗ that satisfies:

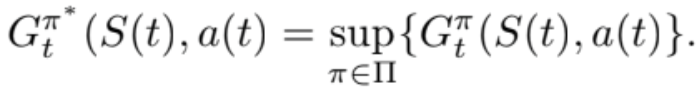
(6)

Algorithm 1 Storage optimization algorithms
Input: Predicted energy demand series: J = {J(1), J(2), …, J(t)}; Discharge threshold: tr; Maximum charging rate: b_max; Minimum charging rate: b_min.
Output: Action series: A = {a(1), a(2), …, a(t)}
Initialisation:

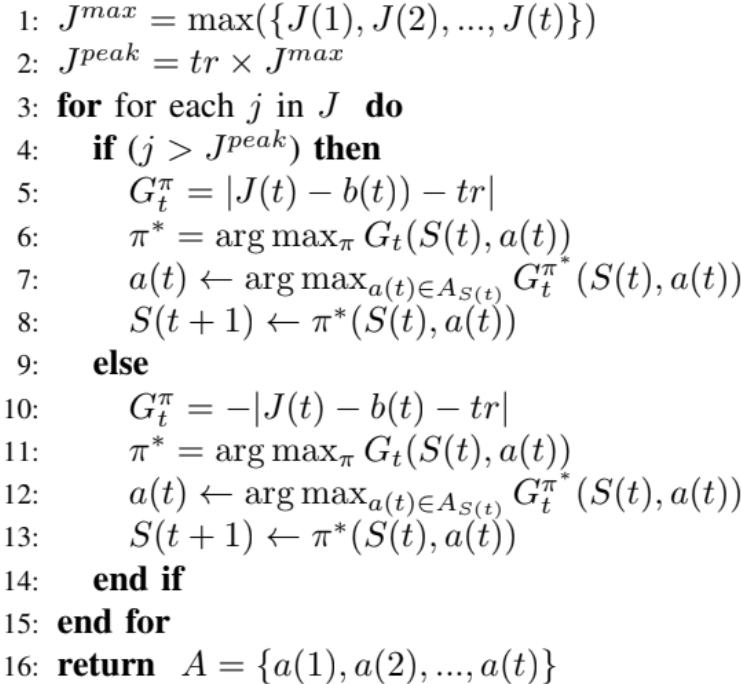
H. Solution Technique
Due to the dimensions of the problem, states, decisions, and continuous random variables in the model, finding an exact solution to our situation is not practical. Therefore, we solve the peak shaving problem in two stages. In the first stage, we use forecasted data to find the proper charging threshold tr and determine the optimal activation window for the energy storage system. In the second stage, the external condition and decision variables are estimated, with next time actions solved using the inverse induction method. Thus, we find the optimal strategy and objective function value for each case.
1) The first stage: It is crucial to decide the proper value of charging threshold tr. A proper value should fully discharge the energy system at a time-varying rate to best shave the demand peak. During the off-peak period, the energy system should recharge to full capacity without establishing a new demand peak. In order to meet these two conditions the charging threshold tr must satisfy the following conditions:

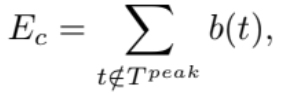
(8)

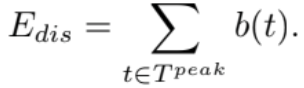
(9)

To account for demand forecasts never being 100% precise, the implemented threshold tr is slightly reduced from the tr

value that maximizes the profit. This preserves safe and reli-
able operation while making the model robust to unexpected environmental stressors.
2) The second stage: As stated, the primary goal can be
formulated as: G_t^π* (S(t), a(t)) = max_π∈Π{G_t^π (S(t), a(t))}. When the time is at peak demand, the goal formulation will be G_t^π* (S(t), a(t)) = max_π∈Π{|J(t) − b(v(t), a(t)) − tr|}. There are two branch sub-situation under this condition: when V_min < v(t) < V_max, G_t^π* = max_π∈Π{|J(t) − e_t^dc − tr|}; When V_min < v(t) < V_max, G_t^π* = max_π∈Π{|J(t) − tr|}. When the time is not at peak demand, the goal formulation will be G_t^π* (S(t), a(t)) = max_π∈Π{−|J(t)−e_t^dc−tr|}. There are also two branch sub-situation under this condition: when V_min < v(t) < V_max, G_t^π* = max_π∈Π{−|J(t)−e_t^dc−tr|}; When v(t) = V_max, G_t^π* = max_π∈Π{−|J(t)−tr|}.
From all above situations, the policy, the action, and the next time state are described as:

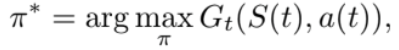
(10)

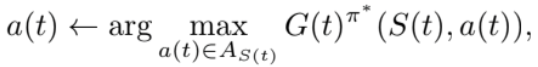
(11)

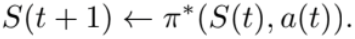
(12)

III. EXPERIMENT RESULTS

In this section, we show how our algorithm manages an energy storage system deployed behind a typical commercial load. We project BTM cost savings to demonstrate the algorithm’s efficacy and justify investment in energy storage.

A. Parameter Setting

The Table II shows the experimental parameters. We consider a 50 kW / 200 kWh on-site energy system that is initially at a fully charged state. The 1:4 ratio of maximum power to total energy is well-suited to demand response programs with 4-hour curtailment requirements. For PHS, the energy capacity depends on the height and volume of the water tank and the maximum power depends on the tank’s outlet. With these small modifications understood, PHS or municipal water management can be handled comparably to battery systems. The daily electricity demand represents a forecast for the summer week of 2021/8/8 to 2021/8/14. The Energy Demand

TABLE II
PARAMETER SETTING AND THE ELECTRICITY RATES

cost is determined by the highest kW value recorded in a 30-minute interval. The Energy Usage cost is determined by the total kWh consumed from the grid.
B. Experiment
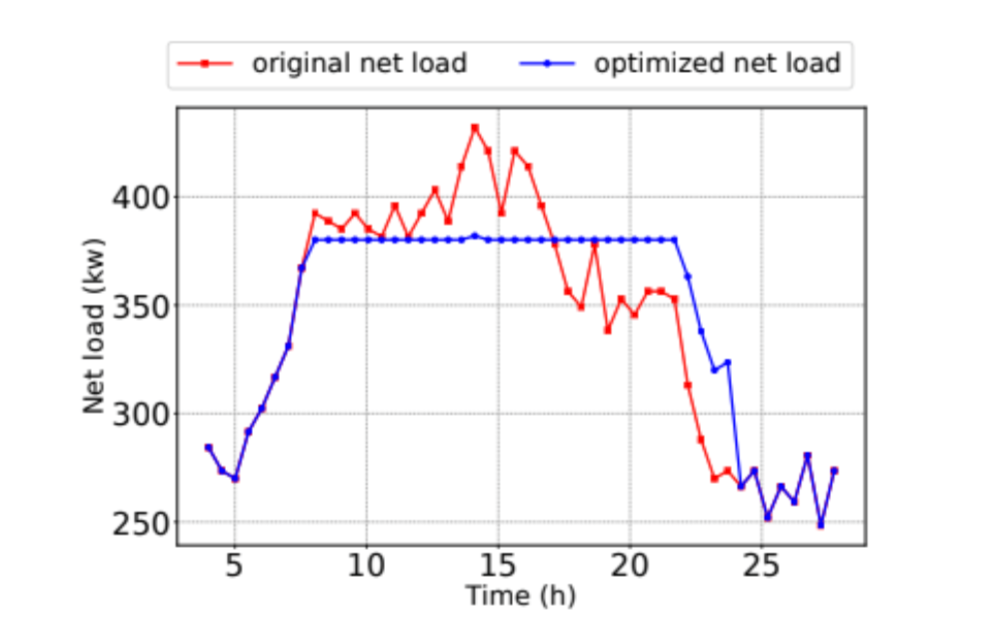
1) One day scale experiment: We first demonstrate how the optimization algorithm can manage an energy storage system over a 24-hour period to shave a demand peak. Figure 2 shows the building’s net load before (red) and after (blue) implementing the optimized energy storage system.
Successful dispatch of stored energy is achieved by lowering the original net load from a peak demand of 430 kW to 382 kW. Assuming the 48 kW peak demand reduction to be sustained for the entire month, the energy storage generates $622 in monthly savings, or $20/day. The algorithm load-shifts the BTM load to reduce the peak demand area by 8%, which benefits systemic energy efficiency. Compared to the original load, the optimized net load increases during low-usage hours in order to recharge the energy storage system to full capacity before the start of the day. As reflected in the demand charge tariff structure, such peak shaving has great value to the electricity consumer and the electric grid.
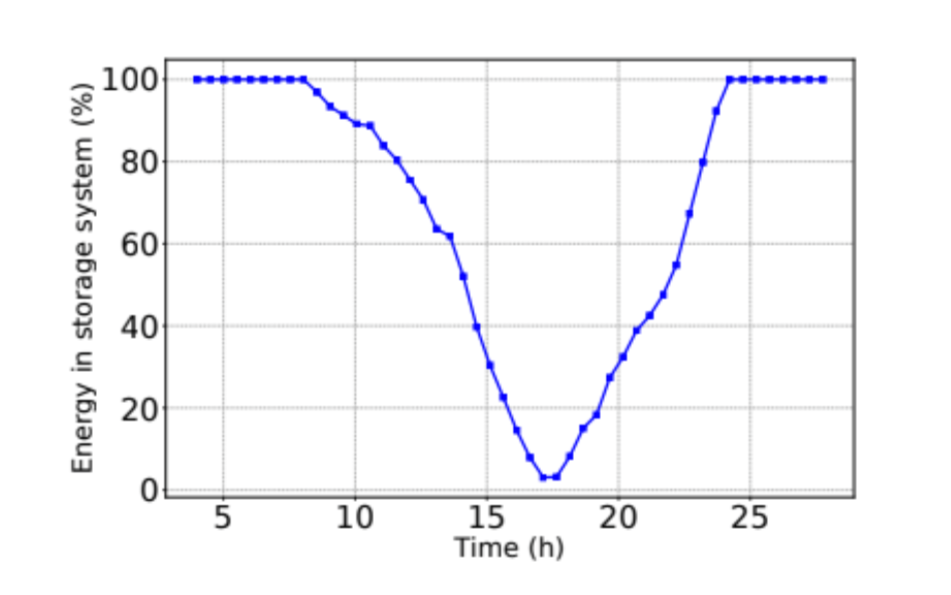
Figure 3 shows the capacity factor of the energy storage system during the optimization procedure in Figure 2. Steady discharging is seen throughout the day, with a minimum capacity of 13% at the end of the discharge period. To allow for easily integrated system protection, a minimum allowable capacity factor can be established. Steady recharging begins when the building’s demand drops below the optimized peak; the system can otherwise be instructed to wait until an off-peak time as dictated by a time-of-use tariff. For highly efficient systems, including PHS, there is minimal cost to the energy arbitrage and we thus neglect energy losses during storage.

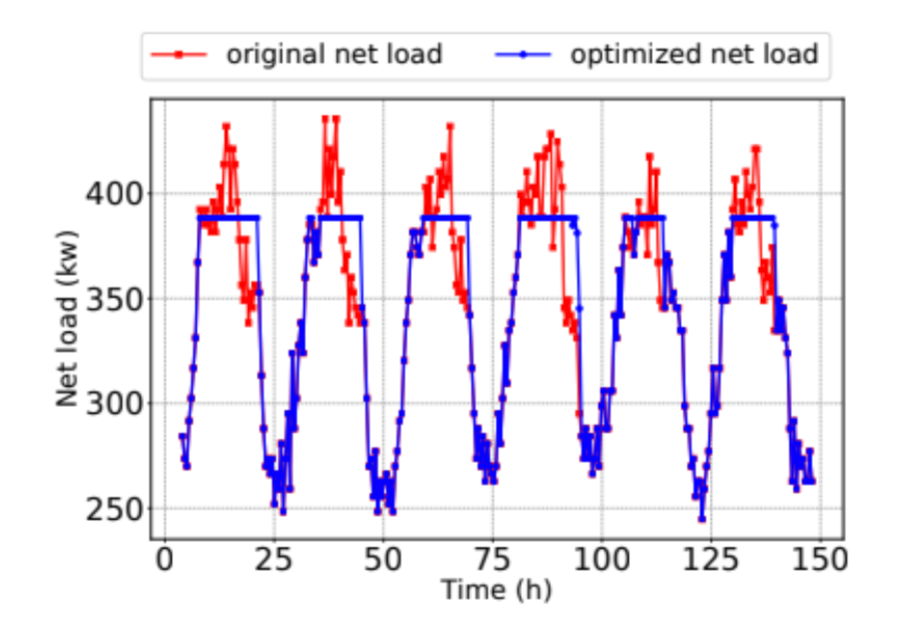
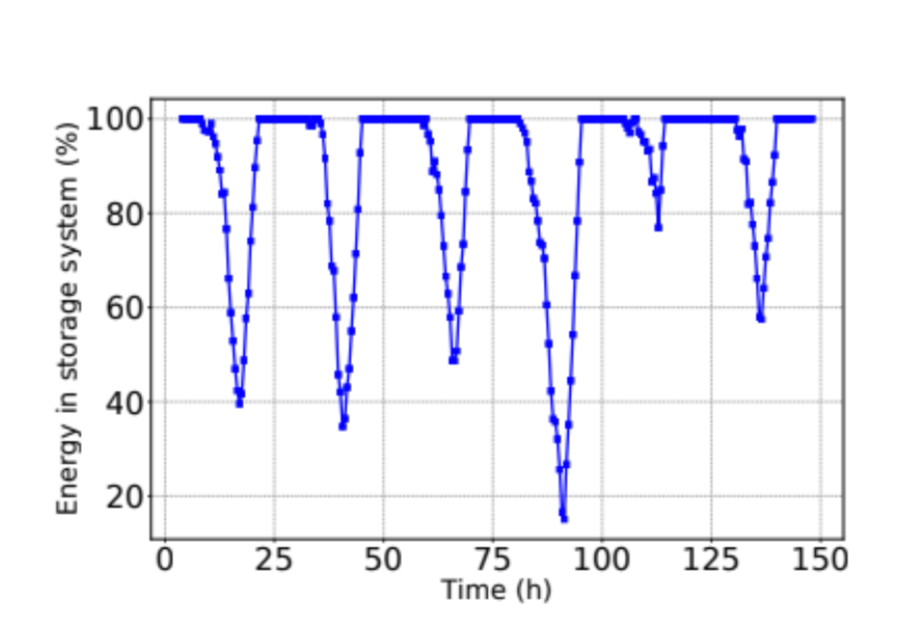
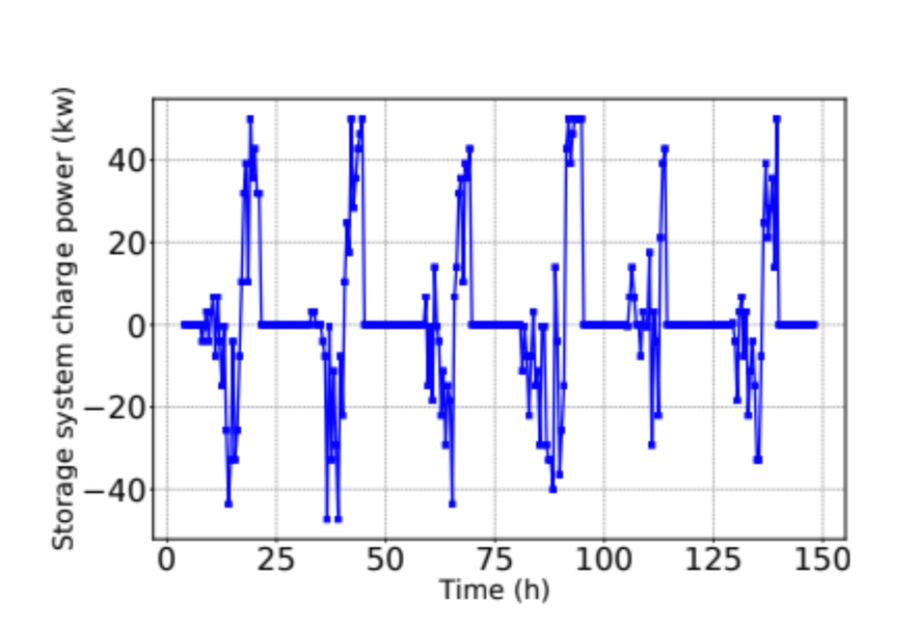
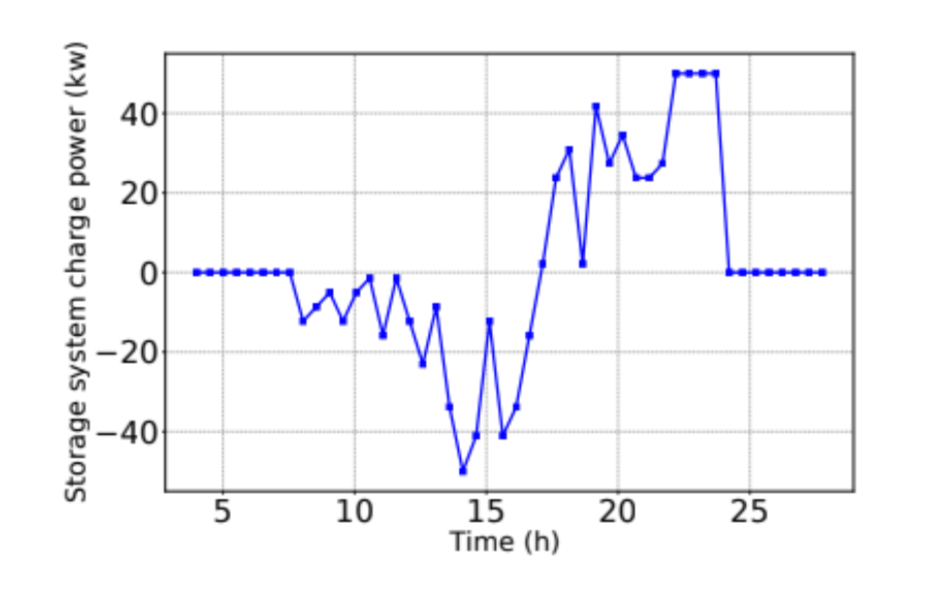
Figure 4 shows the charge and discharge rate of the energy storage system. Between the hours of 8 – 18 the discharge rate is dynamically tuned to best smooth the jagged original energy peak seen in Figure 2. The dynamic discharge is a key feature of the present algorithm and ensures that the customer and the electric system internalize the most value from the storage resource. The maximum charge rate (50 kW) is evident by the flat regions of the curve and is easily tuned to conform to a real system’s parameters (Table II).
2) One week scale experiment: We next demonstrate how the 24-hour procedure scales to longer-term system management by considering 6 days of data.
Figure 5 shows how the optimization algorithm shaves peak load every day. The algorithm establishes a reduced demand peak and then ensures that it is not exceeded on any subsequent day, as seen by the recurrence of flat optimized demands in every peak interval. Such an approach is imperative to internalize monthly savings, as any single-day optimization error would re-establish a high peak.
Figure 6 depicts the capacity factor of the energy system as it operates through the week. The energy storage is recharged to full capacity every night in order to provide resilience and ensure that any daily peak can be shaved. On relatively low-usage days, the system is managed efficiently and discharges by less than 25% (e.g. hour 110). This feature supports system longevity by ensuring that the energy asset is not overused. Alternatively, the excess capacity could be further monetized by selling the energy into day-ahead demand response or ancillary service energy programs.
Figure 7 highlights how smart and time-dependent charge/discharge rates are preserved through the week. The dynamic charging rates allow the system to accommodate random or unanticipated events while optimally managing the net load and storage system capacity. It is seen that the algorithm occasionally instructs for maximum discharge rates (-50 kW) when on-site demand is highest and typically instructs for maximum charge rates (50 kW) during off-peak times. At the transition between peak and off-peak intervals, the power rates can fluctuate between charging/discharging.
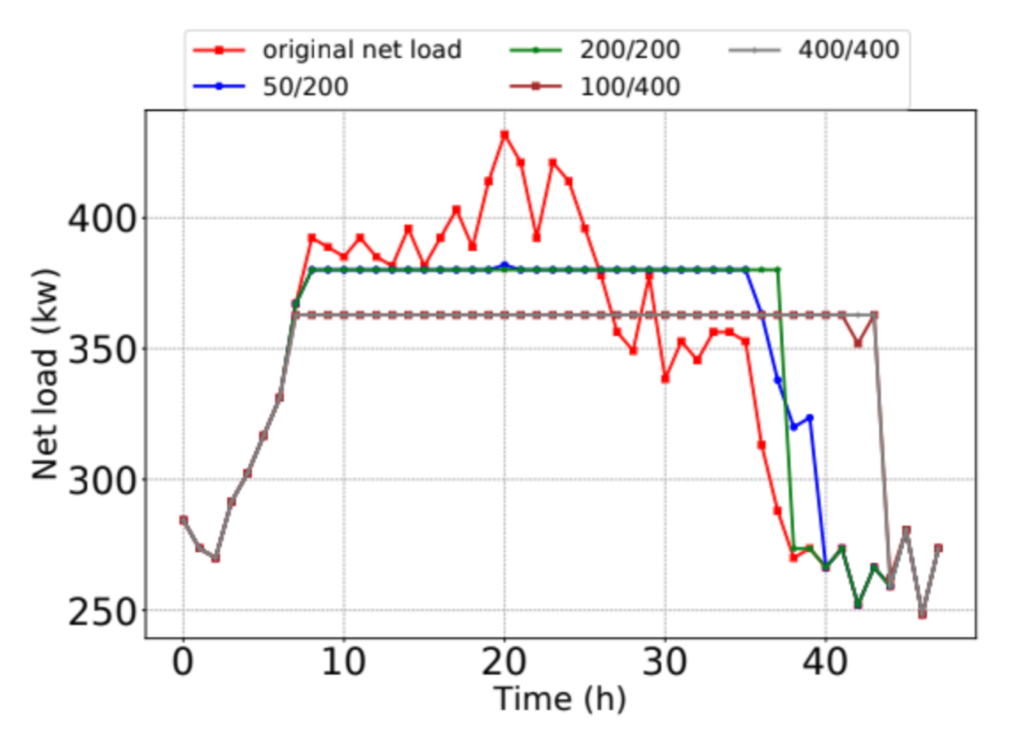
3) Impact of the maximum power rate: To explore how the model can inform on storage system sizing, we compare the 50 kW / 200 kWh system to other power/capacity sizes, specifically 200/200, 100/400, and 400/400. Note that such

larger systems require more costly inverters (or comparable pieces) and volumes of storage elements. From Figure 8, we can see that the original system performs comparably to the larger (more expensive) alternatives. With a constant 200 kWh energy capacity, sizing a 50 kW inverter up to 200 kW is not a justifiable investment for peak-shaving purposes. Similarly, the 2x system size increase to 100/400 only yields a 70 kW reduction in the peak demand (1.46x when compared to the original size). Doubling the size of the energy storage system does not provide 2x savings because an energy duration limit is introduced. In other words, the widening of the demand peak below the 380 kW level means that the 400 kWh capacity limit (rather than the 100 kW power limit) precludes the system from providing sufficient energy for 2x peak shaving when compared to the base case.

4) Impact of the discharge threshold: To highlight the importance of peak and off-peak classification, we conduct experiments on the impact of the discharge threshold value. The below figures show the comparison results among our balanced threshold (88%) versus tresholds at 90% and 70% of the maximum net load.
Figure 9 shows the net load and raw net load between three different thresholds. When the threshold is too low (70%), the energy storage system is overloaded and the energy is exhausted before the peak period ends. On the contrary, when the threshold is too high (90%), the energy storage system is underutilized and retains much energy after the peak demand

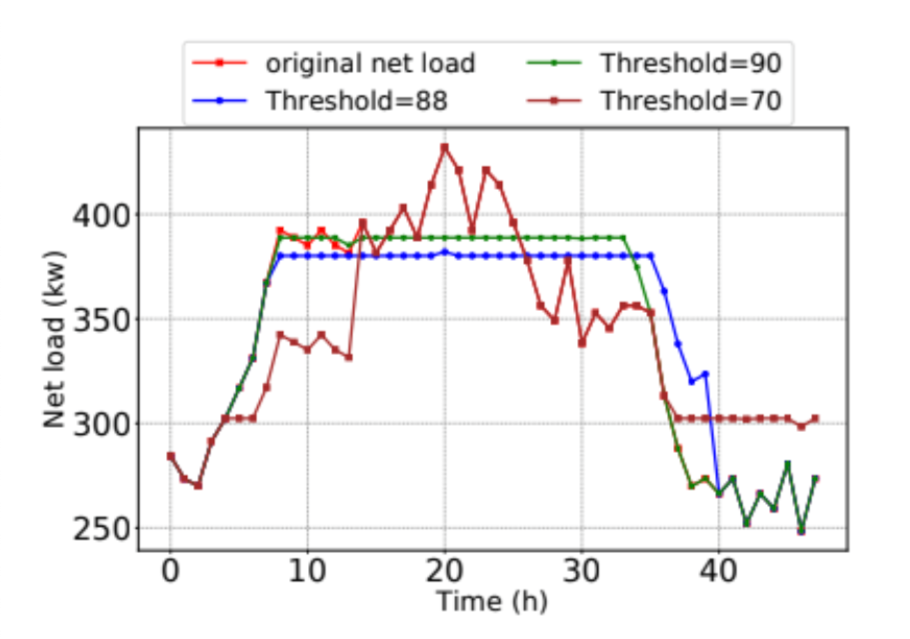
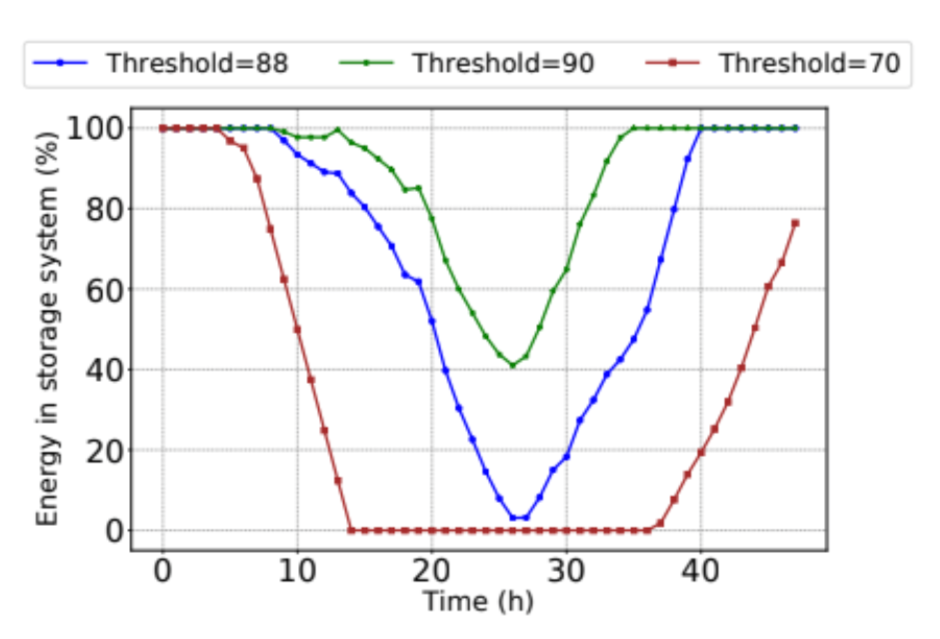
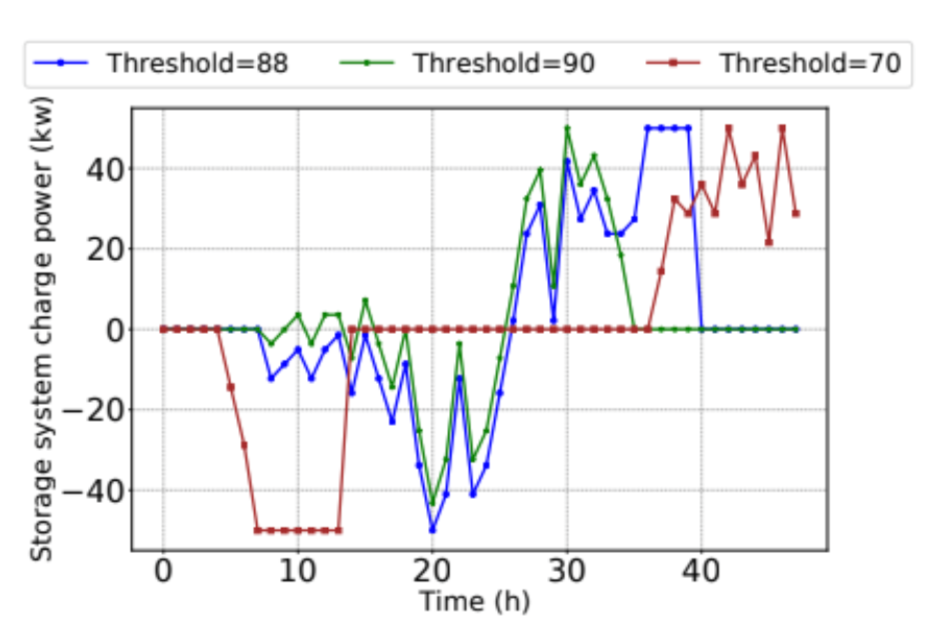
period has passed. These observations are made clear in Figure 10 and Figure 11. The data demonstrate that only a narrow range of threshold values can balance the competing goals of minimizing demand spikes while preventing overloading of the system.

IV. CONCLUSION

A Markov decision process-based optimization algorithm has been demonstrated for behind-the-meter energy storage systems. The algorithm considers a building’s demand profile and the size of an energy storage system to manage charging and discharging for peak shaving. With everyday shaving of a building’s peak demand, the algorithm can reduce on-site electricity costs and systemic peak loads on the grid. We further exploit the algorithm to investigate optimal energy storage system sizing. We show how the building’s demand profile will dictate the optimal system size and how energy duration limits mean that bigger is not always better. Finally, we show how the classification of a time increment as being on-peak or off-peak is the crucial parameter driving successful system optimization. This technology-agnostic optimization can serve battery energy storage systems as well as pumped hydro energy storage, thermal energy storage, and municipal water infrastructure with distributed and elevated tanks. Future works can explore how co-optimization with other energy-intensive assets (e.g. HVAC, lighting, cold storage) or with cues from the electric grid operator (e.g. demand response in wholesale energy or ancillary service programs). These innovations help project and deliver a maximized return on investment for energy storage solutions.

REFERENCES

[1] A. B. Awan, M. Zubair, G. A. S. Sidhu, A. R. Bhatti, and A. G. Abo-Khalil, “Performance analysis of various hybrid renewable energy systems using battery, hydrogen, and pumped hydro-based storage units,” International Journal of Energy Research, vol. 43, no. 12, pp. 6296–6321, 2019.

[2] A. Kaabeche and R. Ibtiouen, “Techno-economic optimization of hybrid photovoltaic/wind/diesel/battery generation in a stand-alone power system,” Solar Energy, vol. 103, pp. 171–182, 2014.

[3] W. Tong, Wind power generation and wind turbine design. WIT press, 2010.

[4] T. Ma, H. Yang, and L. Lu, “Performance evaluation of a stand-alone photovoltaic system on an isolated island in hong kong,” Applied Energy, vol. 112, pp. 663–672, 2013.

[5] B. Bhargava and G. Dishaw, “Application of an energy source power system stabilizer on the 10 mw battery energy storage system at chino substation,” IEEE Transactions on Power Systems, vol. 13, no. 1, pp. 145–151, 1998.

[6] B. K. Das, N. Hoque, S. Mandal, T. K. Pal, and M. A. Raihan, “A techno-economic feasibility of a stand-alone hybrid power generation for remote area application in bangladesh,” Energy, vol. 134, pp. 775–788, 2017.

[7] B. K. Das, Y. M. Al-Abdeli, and G. Kothapalli, “Effect of load following strategies, hardware, and thermal load distribution on stand-alone hybrid cchp systems,” Applied energy, vol. 220, pp. 735–753, 2018.

[8] F. Vivas, A. De las Heras, F. Segura, and J. Andujar, “A review of energy management strategies for renewable hybrid energy systems with hydrogen backup,” Renewable and Sustainable Energy Reviews, vol. 82, pp. 126–155, 2018.

[9] S. Rehman, L. M. Al-Hadhrami, and M. M. Alam, “Pumped hydro energy storage system: A technological review,” Renewable and Sustainable Energy Reviews, vol. 44, pp. 586–598, 2015.

[10] R. Kelman and D. Harrison, “Integrating renewables with pumped hydro storage in brazil: a case study,” 2019.

[11] A. A. Akhil, G. Huff, A. B. Currier, B. C. Kaun, D. M. Rastler, S. B. Chen, A. L. Cotter, D. T. Bradshaw, and W. D. Gauntlett, DOE/EPRI 2013 electricity storage handbook in collaboration with NRECA. Sandia National Laboratories Albuquerque, NM, 2013, vol. 1.

[12] B. Lu, M. Stocks, A. Blakers, and K. Anderson, “Geographic information system algorithms to locate prospective sites for pumped hydro energy storage,” Applied energy, vol. 222, pp. 300–312, 2018.

[13] M. Stocks, R. Stocks, B. Lu, C. Cheng, and A. Blakers, “Global atlas of closed-loop pumped hydro energy storage,” Joule, vol. 5, no. 1, pp. 270–284, 2021.

[14] A. Rogeau, R. Girard, and G. Kariniotakis, “A generic gis-based method for small pumped hydro energy storage (phes) potential evaluation at large scale,” Applied energy, vol. 197, pp. 241–253, 2017.

[15] N. Ghorbani, H. Makian, and C. Breyer, “A gis-based method to identify potential sites for pumped hydro energy storage-case of iran,” Energy, vol. 169, pp. 854–867, 2019.

[16] U. E. I. Administration. (2022) Hydropower ex-plained where hydropower is generated. [Online].Available: https://www.eia.gov/energyexplained/hydropower/where-
hydropower-is-generated.php

[17] E. Garc ́ıa and `I. Isaac, “Demand response systems for integrating energy storage batteries for residential users,” in 2016 IEEE Ecuador Technical Chapters Meeting (ETCM). IEEE, 2016, pp. 1–6.

[18] M. L. Puterman, Markov Decision Processes: Discrete Stochastic Dynamic Programming. John Wiley & Sons, 1994.

[19] A. Hassan, S. Acharya, M. Chertkov, D. Deka, and Y. Dvorkin, “A hierarchical approach to multienergy demand response: From electricity to multienergy applications,” Proceedings of the IEEE, vol. 108, no. 9,pp. 1457–1474, 2020.